How To Create Tower Of Hanoi Animation In Matlab

TALK Like A MATHEMATICIAN

Detached MATHEMATICS – the study of mathematical structures that are countable and separable, rather than continuous

EXPONENTIAL – IN MATHEMATICS, CONTAINING AN EXPONENT – a number that shows how many times another number is to be multiplied by itself

FRACTAL – a shape for which any office is a larger or smaller version of another part. Lookout man this BBC Ideas video on YouTube for a detailed explanation: https://www.youtube.com/watch?five=w_MNQBWQ5DI

RECURSION – the repeated awarding of a procedure that involves breaking down the procedure into smaller, similar parts

TOWER OF HANOI – a mathematical puzzle involving moving a tower of discs from one pole to another, while obeying sure rules

In 1883, a French mathematician named Édouard Lucas came upward with an intriguing scenario. There are three poles in a row, the ane on the left containing a series of discs of decreasing size, with the other two, empty. The aim is to move the tower, one disc at a time, over to the right-mitt pole. Nevertheless, the catch is, a larger disc can never sit on top of a smaller disc. This puzzle chop-chop reached fame as the brainteaser now known every bit the Belfry of Hanoi.

Despite it seeming initially perplexing, in truth the Tower of Hanoi is a problem that even amateur puzzlers can solve with a bit of lateral thinking. However, underlying the puzzle are some key mathematical ideas – even if we might not appreciate them when solving information technology. Professor Dan Romik, of the University of California, Davis, has investigated the Tower of Hanoi and, despite the puzzle's apparent simplicity, has shown that it continues to yield new surprises.

RECURSION

"Recursion is the extremely useful idea of solving a big trouble past reducing it to smaller instances of the same problem," says Dan. For instance, imagine you have eighty coins and a prepare of balance scales. All the coins weigh the same, autonomously from one that weighs slightly less. To find this lighter coin, one solution would exist to weigh and compare two coins at a time to come across if in that location is any departure in weight – but this method would take ages. A faster way would be to divide the pile into two piles of twoscore and weigh these 2 piles against 1 another. You tin can select the lighter pile and discard the other twoscore coins all at once. Y'all so repeat this process, dividing the pile into two twenties, 2 tens, and then on, until you narrow it downward to the one coin.

The Tower of Hanoi tin be solved using recursion too, which helps mathematicians notice the manner to solve the puzzle in the fewest number of steps possible. Ultimately, it involves constructing and reconstructing progressively larger 'towers', until the bottom disc tin be moved to the 3rd pole and the rest of the tower constructed upon it, every bit the text box explains in mathematical terms (See 'Solving the Tower of Hanoi through recursion' on the third page). The more than discs that the puzzle contains, the more steps information technology will take – rise exponentially, in fact. This can be written in algebraic course: Southward = 2^{Due north}-ane

In this formula, South is the number of steps, and Northward is the number of discs. So, if the tower had 5 discs, the formula would be 25-1, which is 31. Therefore, solving the puzzle would take a minimum of 31 steps. If information technology had 4 discs, information technology would require but xv steps – and for iii discs, only 7.

Interestingly, this formula can lead us dorsum to the Tower of Hanoi's supposed mythological roots. The legend goes that immature priests of a Hindu temple were tasked with moving discs of pure gold according to the rules of the puzzle – except that their Tower contained not 5 but 64 discs, and it was said that when they completed the task, the world would stop. Using the formula above, we can deem that this is highly unlikely, given it would take them many billions of years to complete! Since this fable was invented past Lucas every bit a marketing ploy, it is hardly surprising that the underlying mathematics do non allow this apocalyptic prophecy to exist put to the test.

GRAPHICAL REPRESENTATION

To visualise not only how many steps are needed, but exactly which steps too, the Tower of Hanoi configuration can be represented on a diagram that mathematicians call a graph. Graphs uncover aspects of a particular scenario that might have otherwise gone unseen, in particular by connecting them to other scenarios that may be better understood. "Many problems in discrete mathematics tin be translated onto a graph, such as scenarios that involve flipping a switch or making a motility in chess," says Dan. "One time you have represented the problem this style, you can spot connections to other bug you already know nearly."

This mode of thinking originated when mathematician Leonhard Euler was tasked with the '7 Bridges of Königsberg' claiming in 1736. Königsberg was a Prussian city bisected by a river that contained two large islands. The four areas betwixt the islands and the 2 sides of the city were connected past seven bridges. Euler'southward challenge was to find a route through the city that involved crossing all seven of the urban center's bridges exactly once. He realised that the simplest manner to approach the problem was to correspond it as a graph, where lines (the bridges) connected four points (the banks and islands) in a mode representative of the metropolis's bodily layout. In one case he had done this, he was able to easily demonstrate that the challenge was impossible. Run into the prototype on the right.

"The thought of representing collections of objects as graphs was a revolutionary one at the time it was invented, and remains incredibly useful," says Dan. A like simplification procedure can have place for the Tower of Hanoi. Whatsoever possible layout of the discs can be represented using a sequence of numbers. For instance, a Tower with three discs can be represented with a  sequence of three numbers, going from the largest to smallest disc. The pole each disc is upon is represented by the value: pole 1, 2 or 3. For example, the sequence '113' ways that the smallest disc is on the third pole and the two larger discs are on the first pole.

These sequences can be used to map out any possible steps from any position – for example, from '111' y'all tin get to '112' or '113'. These and then branch out into other possibilities. It turns out that when all these possibilities are laid out, they can be represented in a very satisfying format – see the epitome below.

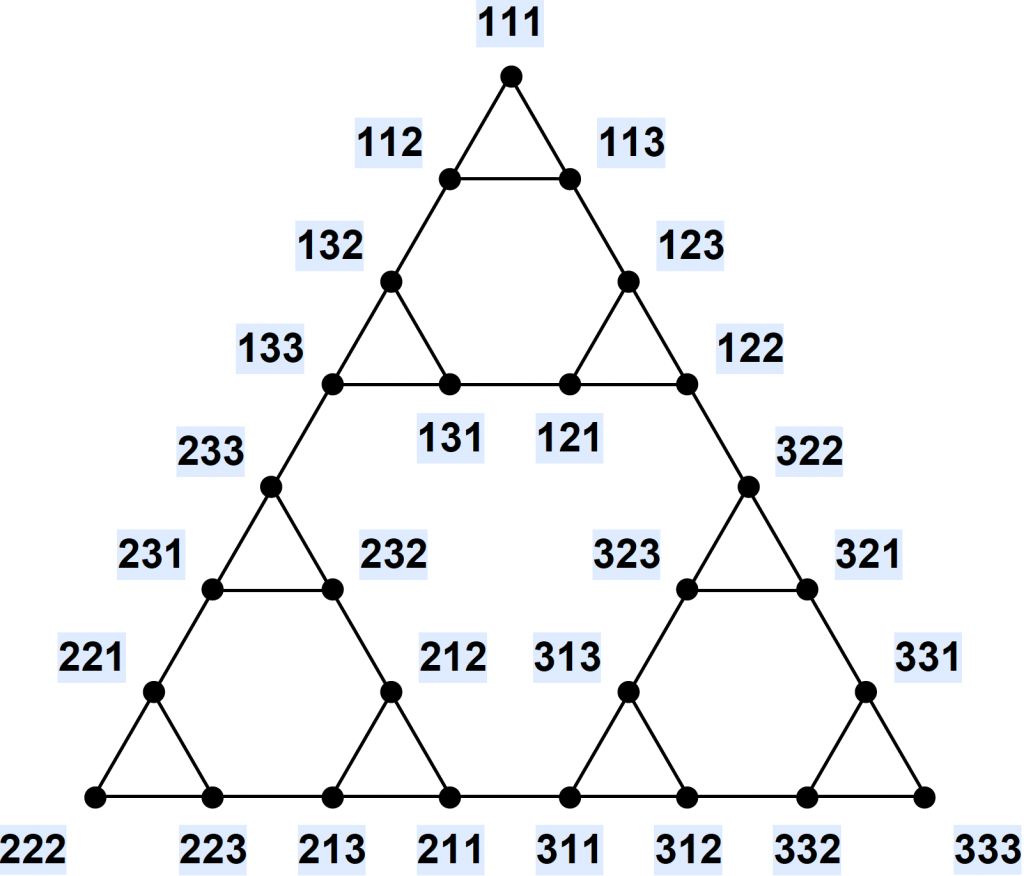
As well as being visually pleasing, this also makes it very easy to find the simplest way to consummate the puzzle by finding the shortest route from '111' to '333'. In fact, this logic tin can be practical to see how to become from one detail configuration to any other.

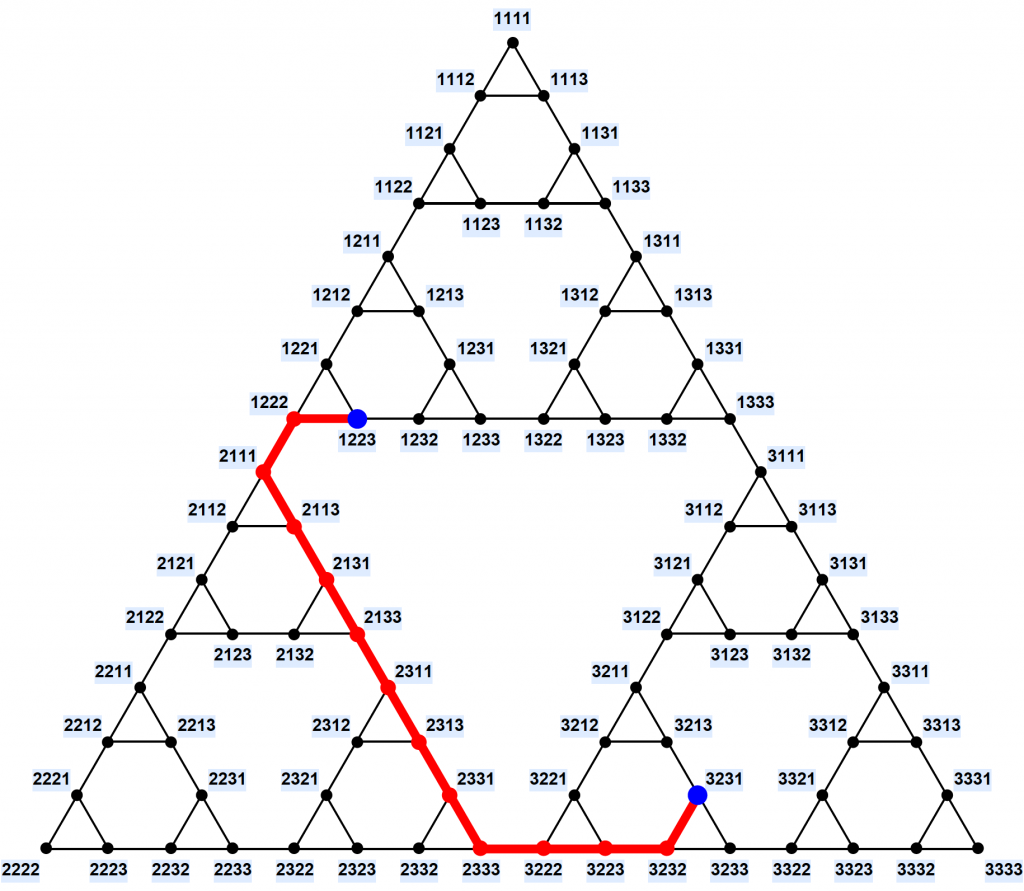
And there is more – because of the Tower'southward underlying recursive construction, its associated graph is not just whatsoever elementary graph, but is as well a fractal. "The puzzle has turned out to be much more interesting than its inventor probably suspected," says Dan.

FRACTALS

A fractal is a geometric shape that, loosely speaking, contains patterns that echo themselves at many different scales. Fractals are oftentimes very appealing to the homo eye and can be often found in nature – think virtually the branches of a tree, and how each is like a miniature tree with sub-branches of its ain. Fractals are also a useful concept for solving mathematical issues. "Fractals frequently announced in mathematical problems where an object can be broken upwardly into several pieces that are similar to but smaller than the original object," says Dan.

The Belfry of Hanoi is an elegant example of this fractal representation. Researchers in the 1980s noticed that when you graphically correspond the steps within a Tower of Hanoi puzzle of any number of discs, you lot stop upwardly with something resembling a well-known fractal commencement described in 1915 for unrelated reasons: the Sierpiński triangle. Yous can run into the resemblance for yourself below or in this animation, hither:

http://math.ucdavis.edu/~romik/downloads/hanoi-animation.gif

"Mathematics is about discovering patterns in the world around us," says Dan. "The near interesting sorts of patterns to detect are those that reveal that two concepts are related to each other, when beforehand no link between them we known. That's when you know you lot've hitting on a genuinely new idea."

SHORTEST PATHS

Solving the Belfry of Hanoi puzzle is tantamount to finding a shortest path in the graph between the '11…ane' state and the '33…three' country. If someone easily y'all the puzzle after scrambling it to some weird configuration and asks you to bring information technology to some desired final state, you can exercise this past tracing out a shortest path in the graph between the sequences corresponding to the starting and ending states (see the figure below).

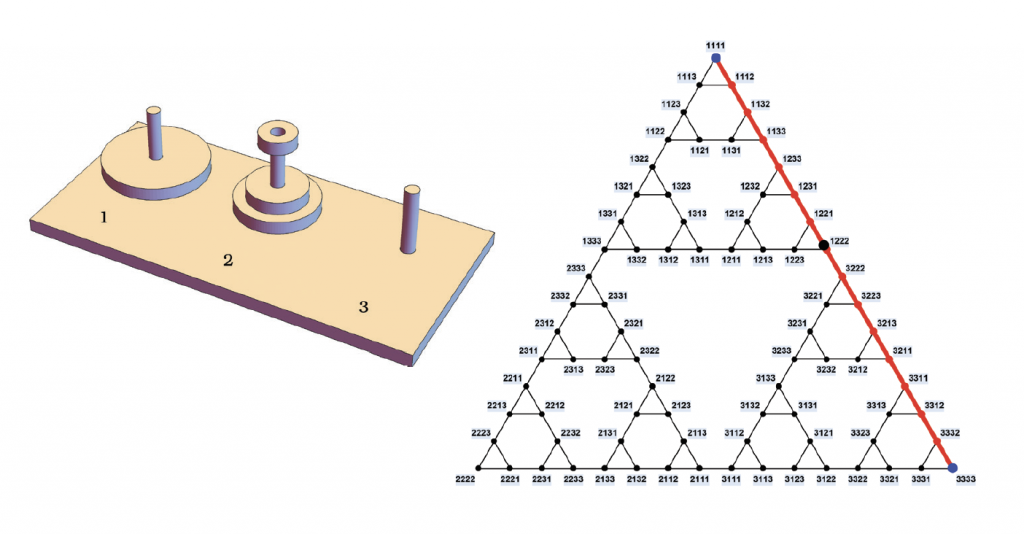
Dan's inspiration to work on the Tower came after reading about the work of mathematician Andreas Hinz, who worked out a formula describing the average number of steps to become describing the average number of steps to become from 1 random configuration of the puzzle to another — that is, the boilerplate length of a shortest path connecting two random states of the puzzle. While in the worst possible instance the number of steps would be 2N-ane (which happens when both the initial and terminal states happens when both the initial and final states have all the discs concentrated on one pole, as in the original trouble), Hinz'southward formula says that for full general initial and final states, the number of steps required would be, on average, only 466/885 times 2N, or approximately 52.half dozen% the number of steps of the worst instance. (N is the number of discs).

"I was intrigued by the weirdness of Hinz's formula and the appearance of the foreign number 466/855 and decided to look at Hinz's paper describing his ideas," says Dan. "When I did and tried to understand his adding, I realised I could ameliorate on it in a small mode and get a meliorate understanding of where the number 466/885 comes from, and ended up writing my own newspaper on the subject. It was essentially a chance discovery driven by zero more than than curiosity."

The idea of shortest paths is very satisfying, but what practise these paths mean for the existent earth? "The Tower of Hanoi graph is a flake bogus to exist of much applied use," says Dan. "However, shortest paths in general are enormously important these days." For case, when nosotros apply SatNav, the SatNav's software is literally finding a shortest path betwixt two points in a graph. Shortest path algorithms are used by companies like UPS and Amazon to send packages in the nearly efficient mode and by cyberspace providers to route the text messages you send to your friends at a minimal price – and in many other situations.

A GATEWAY TO MATHEMATICAL CONCEPTS

The Tower of Hanoi may not announced to accept much real-world awarding, but it is beautiful, somewhat mysterious, and, as it happens, also acts as a gateway to a lot of extremely useful mathematical concepts – recursion, graphical representation and fractals amid them. "Pure mathematics sometimes seems like it's about the pursuit of knowledge that's fun merely useless, simply it'southward of import to allow yourself to follow your curiosity," says Dan. "In that location are many examples where major discoveries were made by mathematicians thinking nearly topics that might accept appeared frivolous or self-indulgent. Following their curiosity meant that the globe was fabricated richer through cool discoveries."

SOLVING THE Belfry OF HANOI THROUGH RECURSION

To move the N discs from pole A to pole B with the assistance of pole C, start by moving the tiptop North-1 discs from pole A to pole C (the recursive bit that uses the same algorithm applied to a smaller number of discs; then move the largest disc from pole A to pole B; and then move the smallest N-1 discs from pole C to pole B (a second repetition of the recursive bit).

For an animation that shows this recursive solution in activity, visit: https://www.math.ucdavis.edu/~romik/tower-of-hanoi/

DAN ROMIK
Professor
Section of Mathematics
University of California, Davis, USA

AREAS OF Interest: Combinatorics, Probability, Number Theory

DAN ROMIK
Professor
Department of Mathematics
University of California, Davis, USA

AREAS OF Involvement: Combinatorics, Probability, Number Theory

HOW TO Become A MATHEMATICIAN

• Equally well as academia, at that place are many organisations that offer mathematics-based apprenticeships or internships. Examples include Microsoft, NASA and MathWorks.

• According to Indeed, the boilerplate annual salary for a mathematician in the US is around $93k.

PATHWAY FROM School TO MATHEMATICIAN

Unsurprisingly, mathematics (and further mathematics, if available) is the most useful subject to study at school to go on to a caste in mathematics. Other useful subjects are physics, chemistry, biology and computer programming. While not mostly required, also taking a humanities subject can aid broaden your skillset.

A degree in mathematics can open doors to a huge and growing range of careers. Many computer programmers, analysts, economists, software developers and data scientists come up from mathematical backgrounds, to name a few.

Do you have a question for Dan?
Write it in the comments box below and Dan will go dorsum to you. (Remember, researchers are very decorated people, so you lot may have to wait a few days.)

Source: https://futurumcareers.com/solving-the-tower-of-hanoi

Posted by: chapmancorgunts.blogspot.com

Share this post